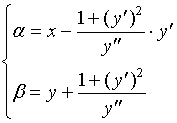§3.9
曲率
一、弧微分
1、有向曲线与有向线段的概念
给定曲线![]() ,取曲线上一固定点
,取曲线上一固定点![]() 作为度量弧长的基点。规定:曲线的正向为依
作为度量弧长的基点。规定:曲线的正向为依![]() 增大的方向。
增大的方向。
对曲线上任一点![]() ,弧段
,弧段![]() 是有向弧段,它的值
是有向弧段,它的值![]() 规定如下:
规定如下:
(1)、![]() 的绝对值
的绝对值![]() 等于该弧段的长度。
等于该弧段的长度。
(2)、当有向弧段![]() 的方向与曲线正向一致时,
的方向与曲线正向一致时,![]() ,相反时
,相反时 ![]() 。
。
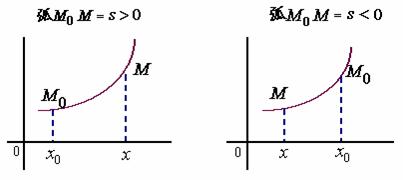
有向弧段![]() 以后简称弧
以后简称弧![]() 。显然,弧
。显然,弧![]() 是
是![]() 的函数,即
的函数,即![]() ,而且是
,而且是![]() 的单调增加函数。
的单调增加函数。
【例1】求曲线![]() 的弧
的弧![]() 。
。
解:选择![]() ,对其上任一点
,对其上任一点![]() ,弧
,弧![]() 的长度是
的长度是 ![]() 。依弧
。依弧![]() 的规定有:
的规定有:
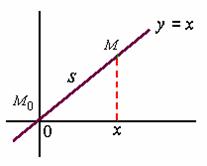
若![]() 在
在![]() 的右侧,即
的右侧,即![]() ,则
,则![]() ,应取
,应取 ![]() ;
;
若![]() 在
在![]() 的左侧,即
的左侧,即![]() ,则
,则![]() ,应取
,应取 ![]() 。
。
总之,![]() ,显然弧
,显然弧![]() 确为
确为![]() 的单增函数。
的单增函数。
2、弧的导数与微分
设函数![]() 的导函数
的导函数![]() 在
在![]() 上连续,又设
上连续,又设![]() ,
, ![]() 为
为![]() 内两点,在曲线上的对应点分别为
内两点,在曲线上的对应点分别为![]() 与
与![]() ,取为曲线上的一固定点为
,取为曲线上的一固定点为![]() 。再设对应于
。再设对应于![]() 的增量
的增量![]() ,弧
,弧![]() 的增量为
的增量为![]() ,有
,有
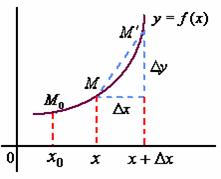
![]()
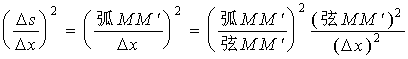
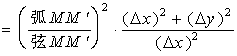
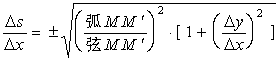
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
, ![]()
故 ![]()
因![]() 是
是![]() 的单调函数,根号前应取正号,于是
的单调函数,根号前应取正号,于是
![]() 或
或 ![]()
进一步地改写可得弧微分公式

![]() 所代表的几何意义如下图所示:
所代表的几何意义如下图所示:
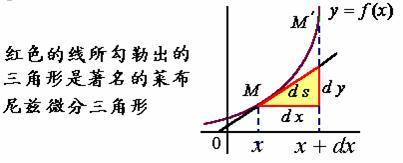
二、曲率及其计算公式
1、曲率的概念
直觉与经验告诉我们:直线没有弯曲,圆周上每一处的弯曲程度是相同的,半径较小的圆弯曲得较半径较大的圆要厉害些,抛物线在顶点附近弯曲得比其他位置厉害些。
何为弯曲得厉害些? 即: 用怎样的数学量来刻划曲线弯曲的程度呢? 让我们先弄清曲线的弯曲与哪些因素有关。

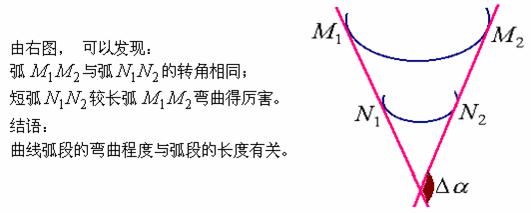
下面,我们给出刻划曲线弯曲程度的数学量 - 曲率的定义。
设曲线![]() 具有连续转动的切线,在
具有连续转动的切线,在![]() 上选定一点
上选定一点![]() 作为度量弧的基点。
作为度量弧的基点。

设曲线![]() 上的点
上的点![]() 对应于弧
对应于弧![]() ,切线的倾角为
,切线的倾角为![]() ,曲线上的另一点
,曲线上的另一点![]() 对应于弧
对应于弧![]() ,切线的倾角为
,切线的倾角为![]() 。那么,弧段
。那么,弧段![]() 的长度为
的长度为 ![]() ,当切点从
,当切点从![]() 移到点
移到点![]() 时,切线转过的角度为
时,切线转过的角度为 ![]() 。
。
比值![]() 表示单位弧段上的切线转角,刻划了弧
表示单位弧段上的切线转角,刻划了弧![]() 的平均弯曲程度。称它为弧段
的平均弯曲程度。称它为弧段![]() 的平均曲率。记作
的平均曲率。记作 ![]() 。
。
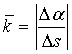
当![]() 时(即:
时(即:![]() ),上述平均曲率的极限就称着曲线在点
),上述平均曲率的极限就称着曲线在点![]() 处的曲率,记作
处的曲率,记作![]() 。
。
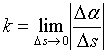 (1)
(1)
当![]() 存在时,有
存在时,有 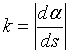 。
。
由上述定义知,曲率是一个局部概念,谈曲线的弯曲应该具体地指出是曲线在哪一点处的弯曲,这样才准确。
2、曲率的计算
【例2】求半径为![]() 的圆上任一点处的曲率。
的圆上任一点处的曲率。
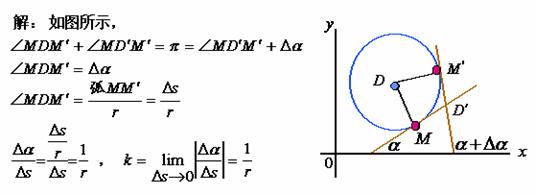
圆周上的任一点处的曲率均为![]() ,这表明:圆周的弯曲程度处处一样, 且半径较小的圆周弯曲得更厉害些。
,这表明:圆周的弯曲程度处处一样, 且半径较小的圆周弯曲得更厉害些。
由例一可发现,利用曲率定义来计算曲率十分不便。下面,我们来推导曲线的曲率计算公式。
设曲线的直角坐标方程为 ![]() ,且
,且![]() 具有二阶导数。
具有二阶导数。
![]() (
(![]() 是曲线的切线与
是曲线的切线与 ![]() 轴正向夹角)
轴正向夹角)
两边对
![]() 求导得
求导得 ![]()
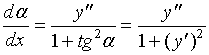 ,
, 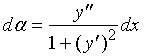
又 ![]()
据曲率计算公式(1)有:
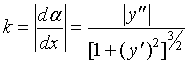 (2)
(2)
若曲线为直线![]() ,因
,因![]() ,那么
,那么 ![]() 。故直线的曲率为零。亦即:直线无弯曲。这与我们的常识是一致的。
。故直线的曲率为零。亦即:直线无弯曲。这与我们的常识是一致的。
假设曲线方程是参数方程 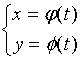 给出
给出
则(2)式可相应地改成形式:
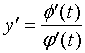 ,
,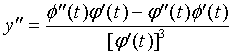 ,
,
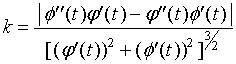 (3)
(3)
【例3】求抛物线![]() 上任一点的曲率。
上任一点的曲率。
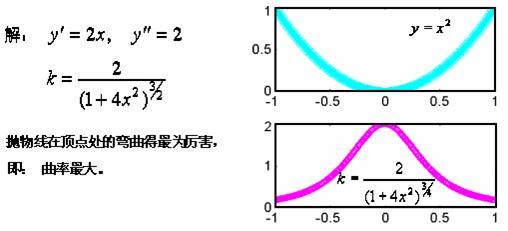
运行程序gs0304.m,可获得抛物线与其曲率函数的图象。
【例4】求立方抛物线![]() 上任一点的曲率。
上任一点的曲率。
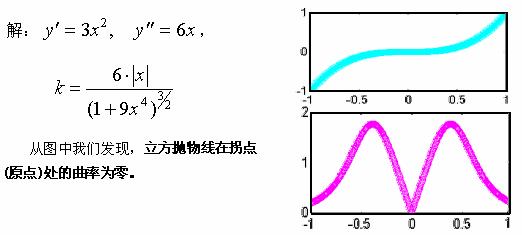
运行程序gs0305.m,可得立方抛物线与它的曲率函数的图象。

三、曲率圆与曲率半径
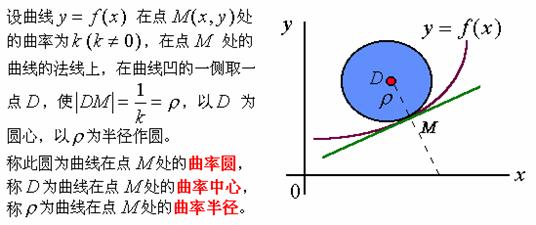
据上述定义有:
1、曲率与曲率半径的关系为:![]()
2、曲线与它的曲率圆在同一点处有相同的切线,曲率,凹向。因此,可用圆率圆在点处的一段圆弧来近似地替代曲线弧。
下面推导曲率圆中心![]() 的坐标计算公式。
的坐标计算公式。
设![]() 的坐标为
的坐标为![]() ,曲线
,曲线![]() 在点
在点![]() 处的曲率圆方程为
处的曲率圆方程为
![]()
其中:![]() 是动点坐标, 而
是动点坐标, 而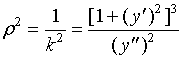 (1)
(1)
因点![]() 在曲率圆上,故
在曲率圆上,故
![]() (2)
(2)
又曲线在点![]() 处的切线与曲率圆的半径
处的切线与曲率圆的半径![]() 垂直,故有
垂直,故有
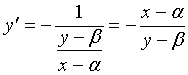 ,
,
亦即:![]() (3)
(3)
![]() (4)
(4)
由式(2)与式(4)消去![]() 得:
得:
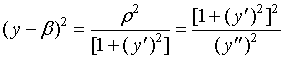
注意到:当![]() ,即曲线为凹弧时,
,即曲线为凹弧时,![]() ;
;
当![]() ,即曲线为凸弧时,
,即曲线为凸弧时,![]() ,
,
总之![]() 与
与![]() 异号,因此,上式两边开方应取“ - ”号,有
异号,因此,上式两边开方应取“ - ”号,有
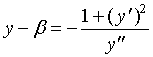
将此式代入(3)式,有
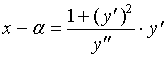 ,从而得
,从而得